바빌로니아 천문학에서 역표를 작성하는 주된 도구는 등차수열이다. 아래 그림은 셀레우시드 시대인 179년(기원전 133-132년)의 역표를 발췌한 것이다.
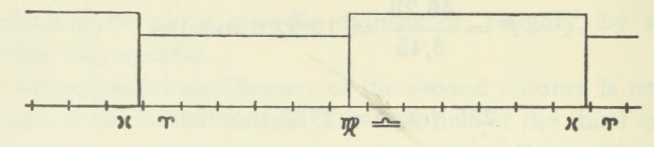
셀레우시드 시대 179년(기원전 133-132년)의 역표
1열은 날짜로 XII2라고 적힌 윤달로 시작되었다. 2,59는 셀레우시드 시대 연도를 표시하고 그 이후 I~XII까지는 그 해의 달을 표시한다.
두 번째 줄부터 뒤의 두 자리는 고정되어 있다. 3행까지는 57, 58, 다음 6행은 21, 22, 다음 4행은 36, 38이다. 그리고 앞의 두 숫자에 주목해 보자. 처음 3행은 2855, 2837, 2819로 18씩 줄어든다. 그 다음에 6행은 18씩 늘어난다. 그 다음에 4행은 18씩 줄어든다.
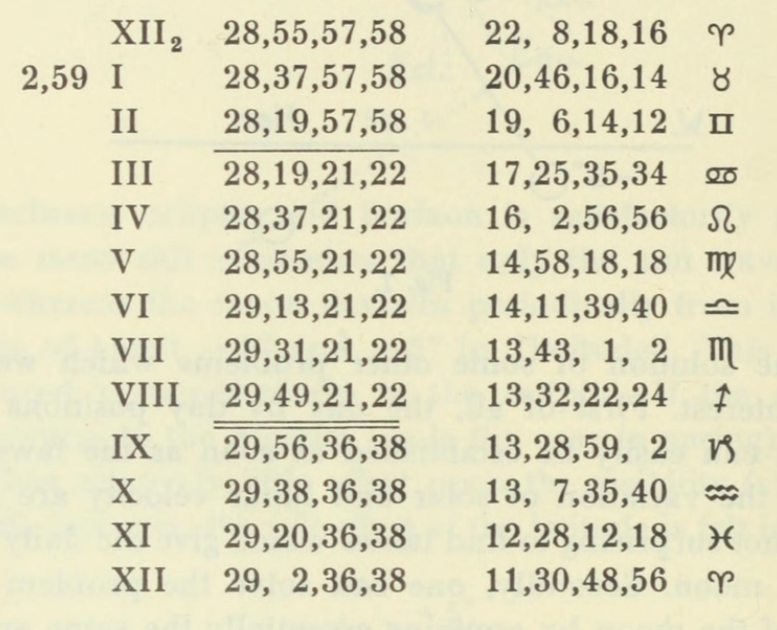
<시스템 B>
이를 그림으로 나타내면 기울기가 +-18인 직선을 얻을 수 있는데, 이를 <선형 지그재그 함수>라 부른다. 가로축은 일정한 간격으로 나누어져 있는데, 각각은 평균삭망월을 나타내고 있다. 선형 지그재그 함수의 최대값 또는 최소값의 주기를 계산하면 약 12와 1/3 삭망월이다.
2열의 천문학적 의미는 3열로 나타난다. 3열 1행은 경도 22; 8, 18, 16의 황도 위치이다. 여기에 2열 2행의 28; 37, 57, 58을 더하면 50; 46, 16, 14가 되며 이는 20; 46, 16, 14가 된다. 이것은 3열 2행의 딱딱함이다. 이렇게 하면 2열은 3열의 차이를 나타낸다. 즉, 3열은 달과 태양의 매달 경도를 나타내고 2열은 매달 태양의 진행 또는 속도를 나타낸다. 따라서 선형 지그재그 함수를 통해 연중해의 속도 변화를 나타내고 있음을 알 수 있다.
<선형 지그재그 함수>를 <시스템 B>라고 부른다. 이는 태양의 속도가 달라진다는 가정하에 만들어졌다.
이것이 전형적인 바빌로니아 천문학이다.
<시스템B>와 대조적으로 해의 속도가 2회씩 교대로 일정하다는 가정 하에 만들어진 것이 <시스템A>이다. 형태상 시스템A가 더 옛날 것으로 보는 학자도 있지만 기록상 동시대에 사용된 것 같다.
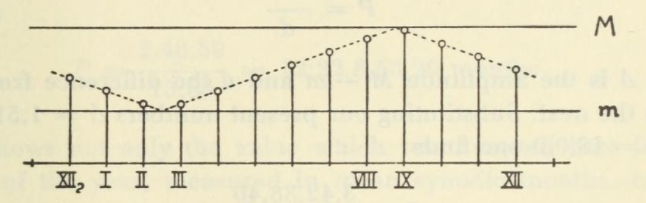
<시스템 A>
이와 같이 모든 역표의 배열은 동일하다. 각 행은 달을 나타내고 각 열은 해와 달의 속도와 같은 함수를 나타낸다.
참고.
Otto Neugebauer , The exact sciences in antiquity